1.1 曲线拟合
用下式来拟合数据.
\[y(x,\mathbb{w}) = w_0 + w_1x + w_2x^2 +... + w_Mx^M = \sum_{j=0}^{M}w_jx^j\]其中M是多项式的阶数(order),$x^j$表⽰x的j次幂。多项式系数$w_0…w_M$整体记作向量w。 注意,虽然多项式函数$y(x,w)$是x的⼀个⾮线性函数,它是系数w的⼀个线性函数。类似多项式 函数的这种关于未知参数满⾜线性关系的函数有着重要的性质,被叫做线性模型
- 过拟合 当我们达到更⾼阶的多项式(M = 9),我们得到了对于训练数据的⼀个完美的拟 合。事实上,多项式函数精确地通过了每⼀个数据点,$E(w) = 0$。然⽽,拟合的曲线剧烈震 荡,就表达函数$sin(2\pi x)$⽽⾔表现很差。这种⾏为叫做过拟合(over-fitting)。
1.2 概率论
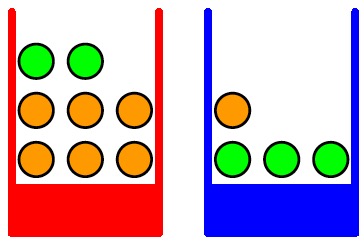 图1.9
图1.9
我们有两个盒⼦,⼀个红⾊的,⼀个蓝⾊的,红盒⼦中有2个苹果和6个橘⼦,蓝盒⼦中有3个苹果和1个橘⼦(如图1.9所⽰)。现在假定我们随机选择⼀个盒⼦,从这个盒⼦中我们随机选择⼀个⽔果,观察⼀下选择了哪种⽔果,然后放回盒⼦中。假设我们重复这个过程很多次。假设我们在40%的时间中选择红盒⼦, 在60%的时间中选择蓝盒⼦,并且我们选择盒⼦中的⽔果时是等可能选择的。 在这个例⼦中,我们要选择的盒⼦的颜⾊是⼀个随机变量,记作B。这个随机变量可以取两个值中的⼀个,即r(对应红盒⼦)或b(对应蓝盒⼦)。类似地,⽔果的种类也是⼀个随机变量,记作F。它可以取a(苹果)或者o(橘⼦).
开始阶段,我们把⼀个事件的概率定义为事件发⽣的次数与试验总数的⽐值,假设总试验次数趋于⽆穷。因此选择红盒⼦的概率为4/10,选择蓝盒⼦的概率为6/10。我们把这些概率分布记作p(B = r) = 4/10和p(B = b) = 6/10。注意,根据定义,概率⼀定位于区间[0, 1]内。并且,如果事件是相互独⽴的,并且包含所有可能的输出(例如在这个例⼦中,盒⼦⼀定要么是红⾊,要么是蓝⾊),那么我们看到那些事件的概率的和⼀定等于1。
我们现在可以问这样的问题:选择到苹果的整体概率是多少?或者,假设我们选择了橘⼦,我们选择的盒⼦是蓝盒⼦的概率是多少?我们可以回答这种问题,事实上也可以回答与模式识 别相关的⽐这些复杂得多的问题。前提是我们掌握了概率论的两个基本规则:加和规则(sum rule)、乘积规则(product rule)。获得了这些规则之后,我们将重新回到我们的⽔果盒⼦的例⼦中。
加和规则和乘积规则
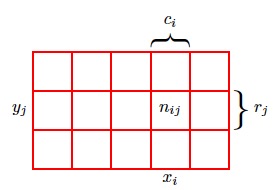 图1.10
图1.10
为了推导概率的规则,考虑图1.10所⽰的稍微⼀般⼀些的情形。这个例⼦涉及到两个随 机变量X和Y (例如可以是上⾯例⼦中“盒⼦”和“⽔果”的随机变量)。我们假设X可以取任意 的$x_i$,其中i = 1 … M,并且Y 可以取任意的yj,其中j = 1 … L。考虑N次试验,其中我们 对X和Y 都进⾏取样,把X = $x_i$且Y = $y_j$的试验的数量记作$n_{ij}$。并且,把X取值$x_i$(与Y 的取 值⽆关)的试验的数量记作$c_i$,类似地,把Y 取值$y_j$的试验的数量记作$r_j$。 X取值$x_i$且Y 取值$y_j$的概率被记作$p(X = x_i, Y = y_j)$,被称为X = $x_i$和Y = $y_j$的联合概率 (joint probability)。它的计算⽅法为落在单元格i, j的点的数量与点的总数的⽐值,即:
\[p(X = x_i, Y = y_j) = \frac{n_{ij}}{N}\]公式(1.5)
这⾥我们隐式地考虑极限$N\mapsto \infty$。类似地,X取值$x_i$(与Y 取值⽆关) 的概率被记 作p(X = $x_i$),计算⽅法为落在列i上的点的数量与点的总数的⽐值,即:
\[p(X=x_i) = \frac{c_i}{N}\]公式(1.6)
由于图1.10中列i上的实例总数就是这列的所有单元格中实例的数量之和,我们有$c_i = \sum_{j} n_{ij}$ 因此根据公式(1.5)和公式(1.6),我们有加和规则:
\[p(X=x_i) = \sum_{j}^{L}p(X=x_i,Y=y_j)\]$p(X = x_i)$有时被称为边缘概率(marginal probability),因为它通过把其他变量(本例中的Y )加总到边缘或者加和得到。(类似excel表格总计一般是统计到表格的边缘). 如果我们只考虑那些$X =x_i$的实例,那么这些实例中$Y =y_j$的实例所占的⽐例被写成$p(Y = y_j|X = x_i)$,被称为给定$X = x_i$的$Y = y_j$的条件概率(conditional probability)。它的 计算⽅式为:计算落在单元格i, j的点的数量与列i的点的数量的⽐值,即
\[p(Y = y_j|X = x_i) = \frac{n_{ij}}{c_i}\]可以推导出乘积规则(product rule)
\[p(X=x_i,Y=y_j) =\frac{n_{ij}}{N}=\frac{n_{ij}}{c_i}.\frac{c_i}{N} = p(Y = y_j|X = x_i)p(X=x_i)\]简记为:
\[p(X)=\sum_Y p(X,Y) p(X,Y) = p(Y|X)p(X)\]| 其中p(X,Y )是联合概率,可以表述为“X且Y 的概率”。类似地,p(Y | X)是条件概率,可以表述为“给定X的条件下Y 的概率”,p(X)是边缘概率,可以简单地表述为“X的概率”。这两个简单的规则组成了我们在全书中使⽤的全部概率推导的基础。 |
由乘法规则, 得到条件概率公式:
\[p(Y|X) = \frac{P(X,Y)}{P(X)}\]根据乘积规则,以及对称性p(X, Y ) = p(Y, X),我们⽴即得到了下⾯的两个条件概率之间的 关系:
\[p(Y | X) = \frac {p(X | Y )p(Y )}{p(X)}\]公式(1.12)
这被称为贝叶斯定理(Bayes’theorem),在模式识别和机器学习领域扮演者中⼼⾓⾊。使⽤加 和规则,贝叶斯定理中的分母可以⽤出现在分⼦中的项表⽰: p(X) = Σ Y p(X j Y )p(Y ) (1.13) 我们可以把贝叶斯定理
1.2.1 连续变量和概率密度
既然考虑了定义在离散事件集合上的概率, 我们也希望考虑与连续变量相关的概 率。我们会把我们的讨论限制在⼀个相对⾮正式的形式上。如果⼀个实值变量x的概率 落在区间$(x, x + \sigma x)$的概率由$p(x)\sigma x$给出$(\sigma x \mapsto 0)$,那么p(x)叫做x的概率密度(probability density)。如图1.12所示,x位于区间$(a, b)$的概率由下式给出
\[p(x \in (a, b)) = \int_{a}^{b}p(x) dx\]可以知道:
\[p(x)>0 \int_{-\infty}^{\infty}p(x)dx=1\]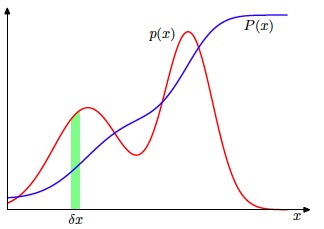 图1.12
图1.12
如果我们有⼏个连续变量$x_1,…,x_D$,整体记作向量$x$,那么我们可以定义联合概率密 度$p(x) = p(x_1,…,x_D)$,使得x落在包含点x的⽆穷⼩体积$\sigma x$的概率由$p(x)\sigma x$给出。多变量概率 密度必须满⾜
\[p(x)>0 \int_{-\infty}^{\infty}p(x)dx=1\]我们也可以考虑离散变量和连续变量相结合的联合概率 分布。 注意, 如果x是⼀个离散变量, 那么p(x)有时被叫做概率质量函数(probability mass function),因为它可以被看做集中在合法的x值处的“概率质量”的集合。 概率的加和规则和乘积规则以及贝叶斯规则,同样可以应⽤于概率密度函数的情形,也可以 应⽤于离散变量与连续变量相结合的情形。例如,如果x和y是两个实数变量,那么加和规则和乘积规则的形式为
\[p(x) = \int p(x)dx p(x,y) = p(y|x)p(x)\]1.2.2 期望和协⽅差
涉及到概率的⼀个重要的操作是寻找函数的加权平均值。在概率分布p(x)下,函数f(x)的平 均值被称为f(x)的期望(expectation),记作E[f]。对于⼀个离散变量,它的定义为
\[E(f) = \sum_x p(x)f(x)\]连续变量 期望定义为:
\[E(f) = \int_x p(x)f(x)dx\]两种情形下,如果我们给定有限数量的N个点,这些点满⾜某个概率分布或者概率密度函数, 那么期望可以通过求和的⽅式估计
\[E(f) = \frac{1}{N}\sum_{n=1}^N f(x_n)\]f(x)的⽅差(variance)被定义为
\[var[f] = E[(f(x)-E[f(X))^2] var[f] = E[f(x)^2-E[f(X)]^2 var[x] = E(x^2)-E(x)^2\]协方差, 对两个变量x,y:
\[cov[x, y] = E_{x,y}[\{x-E[x]\}\{y^T - E[y^T]\}] = E_{x,y}[xy^T]-E[x]E[y^T]\]对向量x,y, 协方差:
\[cov[x, y] = E_{x,y}[\{x-E[x]\}\{y^T - E[y^T]\}] = E_{x,y}[xy^T]-E[x]E[y^T]\]对x向量自身求协方差:
\[cov[x] \equiv cov[x, x]\]1.2.3 贝叶斯概率
我们根据随机重复事件的频率来考察概率。我们把这个叫做经典的 (classical)或者频率学家(frequentist)的关于概率的观点。现在我们转向更加通⽤的贝叶斯 (Bayesian)观点。这种观点中,频率提供了不确定性的⼀个定量化描述。 在⽔果盒⼦的例⼦中,⽔果种类的观察提供 了相关的信息,改变了选择了红盒⼦的概率。在那个例⼦中,贝叶斯定理通过将观察到的数据 融合,来把先验概率转化为后验概率。正如我们将看到的,在我们对数量(例如多项式曲线拟 合例⼦中的参数w)进⾏推断时,我们可以采⽤⼀个类似的⽅法。在观察到数据之前,我们有 ⼀些关于参数w的假设,这以先验概率p(w)的形式给出。观测数据$D = {t_1,…,t_N}$的效果可以 通过条件概率$p(D|w)$表达,我们将在1.2.5节看到这个如何被显式地表达出来。贝叶斯定理的形式为
\[p(w | D) = \frac{p(D | w)p(w)} {p(D)}\]贝叶斯定理右侧的量p(D j w)由观测数据集D来估计,可以被看成参数向量w的函数,被称为似然函数(likelihood function)。它表达了在不同的参数向量w下,观测数据出现的可能性的 ⼤⼩。注意,似然函数不是w的概率分布,并且它关于w的积分并不(⼀定)等于1。 给定似然函数的定义,我们可以⽤⾃然语⾔表述贝叶斯定理
\[posterior \varpropto likelihood \times prior\]-
独立同分布 独⽴地从相同的数据点中抽取的数据点被称为独⽴同分布(independent and identically distributed),通常缩写成i.i.d.
-
最大似然估计 两个独立事件的联合概率等于独立事件的概率的乘积. 那么:
1.5 决策论
概率论是如何提供给我们⼀个⾃始⾄终的数学框架来量化和计算不确定性。当决策论与概率论结合的时候,我们能够在涉及到不确定性的情况下做出最优的决策.考虑⼀下概率论如何在做决策时起作⽤。当我们得到⼀个新病⼈的X光⽚x时,我们的⽬标是判断这个X光⽚属于是否得癌症两类中的哪⼀类。在给定这个图像的前提下,两个类的概率,即$p(C_k|x)$,$C_1$患癌症,$C_2$没患癌症。使⽤贝叶斯定理,这些概率可以⽤下⾯的形式表⽰
\[p(C_k|x) = \frac{p(x|C_k)p(C_k)}{p(x)}\]出现在贝叶斯定理中的任意⼀个量都可以从联合分布$p(x,C_k)$中得到,要么通过积分的⽅式,要么通过关于某个合适的变量求条件概率。
| 把分类问题划分成了两个阶段:推断(inference)阶段和决策(decision)阶段。在推断阶段,我们使⽤训练数据学习$p(C_k | x)$的模型。在接下来的决策阶段,我们使⽤这些后验概率来进⾏最优的分类。另⼀种可能的⽅法是,同时解决两个问题,即简单地学习⼀个函数,将输⼊x直接映射为决策。这样的函数被称为判别函数(discriminant function) |
解决决策问题三种方法
-
对于每个类别$C_k$,独⽴地确定类条件密度$p(x C_k)$。这是⼀个推断问题。然后,推断先验类概率$p(C_k)$。之后,使⽤贝叶斯定理
求出后验概率.
| 我们可以直接对联合概率分布$p(x | C_k)$建模,然后归⼀化,得到后验概率。得到后验概率之后,我们可以使⽤决策论来确定每个新的输⼊x的类别。显式地或者隐式地对输⼊以及输出进⾏建模的⽅法被称为⽣成式模型(generative model),因为通过取样,可以⽤来⼈⼯⽣成出输⼊空间的数据点。 |
-
⾸先解决确定后验类密度$p(C_k x)$这⼀推断问题,接下来使⽤决策论来对新的输⼊x进⾏分类。这种直接对后验概率建模的⽅法被称为判别式模型(discriminative models)。 - 找到⼀个函数f(x),被称为判别函数。这个函数把每个输⼊x直接映射为类别标签。例
如,在⼆分类问题中,f()可能是⼀个⼆元的数值,f = 0表⽰类别$C_1$,f = 1表⽰类别$C_2$。这种情况下,概率不起作⽤。
$$
1.6 信息论
我们考虑⼀个离散的随机变量x。当我们观察到这个变量的⼀个具体值的时候,我们接收到了多少信息呢?信息量可以被看成在学习x的值的时候的“惊讶程度”。 我们对于信息内容的度量将依赖于概率分布p(x),因此我们想要寻找⼀个函数h(x),它 是概率p(x)的单调递增函数,表达了信息的内容。h()的形式可以这样寻找:如果我们有两 个不相关的事件x和y,那么我们观察到两个事件同时发⽣时获得的信息应该等于观察到事 件各⾃发⽣时获得的信息之和,即$h(x, y) = h(x) + h(y)$。两个不相关事件是统计独⽴的,因 此$p(x, y) = p(x)p(y)$。根据这两个关系,很容易看出$h(x)$⼀定与p(x)的对数有关。因此,我们有
公式(1.92)
其中,负号确保了信息⼀定是正数或者是零。注意,低概率事件x对应于⾼的信息量。对数的底 的选择是任意的。现在我们将遵循信息论的普遍传统,使⽤2作为对数的底。在这种情形下,正 如我们稍后会看到的那样,h(x)的单位是⽐特(bit, binary digit)。 现在假设⼀个发送者想传输⼀个随机变量的值给接收者。这个过程中,他们传输的平均信息 量通可以通过求公式(1.92)关于概率分布p(x)的期望得到。这个期望值为
\[H[x] = - \sum_x p(x) log_2 p(x)\]这个重要的量被叫做随机变量x的熵(entropy)。注意,$lim_{p\mapsto 0} p log_2 p = 0$,因此只要我们遇到 ⼀个x使得$p(x) = 0$,那么我们就应该令$p(x) log_2 p(x) = 0$。
示例
考虑⼀个随机变量x。这个随机变量有8种可能的状态,每个状态都是等可能的。为了把x的值传给接收者,我们需要传输 ⼀个3⽐特的消息。
\[H[x] = -8 \times \frac{1}{8} \times log_2 {\frac{1}{8}} = 3 bit\]现在考虑⼀个具有8 种可能状态(a, b, c, d, e,f, g,h)的随机变量, 每个状态各⾃的概率 为( 1/2 , 1/4 , 1/8 , 1/16 , 1/64 , 1/64, 1/64, 1/64)(Cover and Thomas, 1991)。这种情形下的熵为⾮均匀分布⽐均匀分布的熵要⼩。
\[H[x] = 2bit\]我们可以使⽤下⾯的编码串:0、10、110、1110、 111100、111101、111110、111111来表⽰状态(a, b, c, d, e,f, g,h).熵和最短编码长度的这种关系是⼀种普遍的情形。⽆噪声编码定理(noiseless coding theorem)(Shannon,1948)表明,熵是传输⼀个随机变量状态值所需的⽐特位的下界。
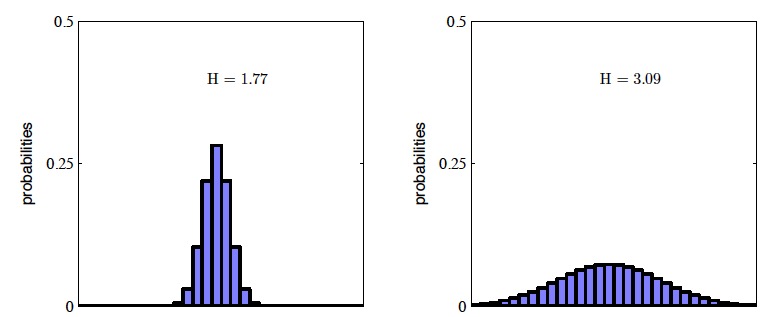 图1.30 两个概率分布在30个箱⼦上的直⽅图,表明熵值越⼤,H越宽。最⼤的熵值产⽣于均匀分布,此
时的熵值为H=-ln(1/30)=3.40
图1.30 两个概率分布在30个箱⼦上的直⽅图,表明熵值越⼤,H越宽。最⼤的熵值产⽣于均匀分布,此
时的熵值为H=-ln(1/30)=3.40
| 假设我们有⼀个联合概率分布p(x,y)。我们从这个概率分布中抽取了⼀对x和y。如果x的值已知,那么需要确定对应的y值所需的附加的信息就是lnp(y | x)。因此,⽤来确定y值的平均附加信息可以写成 |
如非注明转载, 均为原创. 本站遵循知识共享CC协议,转载请注明来源